Baixe aqui o texto completo
Nota divulgada em 25/03/2020
O LEGOS trata o problema de prever a evolução do total de casos confirmados de COVID-19 no município do Rio de Janeiro. Para chegar aos resultados que serão apresentados a seguir utilizamos a série histórica do referido município que está disponível no Painel Rio COVID SMS | IPP | COR. Esta série histórica é apresentada na tabela e figura abaixo.
| Data | Casos confirmados | Data | Casos confirmados |
| 06/03/2020 | 4 | 16/03/2020 | 51 |
| 07/03/2020 | 9 | 17/03/2020 | 60 |
| 08/03/2020 | 12 | 18/03/2020 | 63 |
| 09/03/2020 | 13 | 19/03/2020 | 63 |
| 10/03/2020 | 21 | 20/03/2020 | 94 |
| 11/03/2020 | 25 | 21/03/2020 | 103 |
| 12/03/2020 | 30 | 22/03/2020 | 170 |
| 13/03/2020 | 38 | 23/03/2020 | 214 |
| 14/03/2020 | 42 | 24/03/2020 | 278 |
| 15/03/2020 | 48 | 25/03/2020 | ?? |
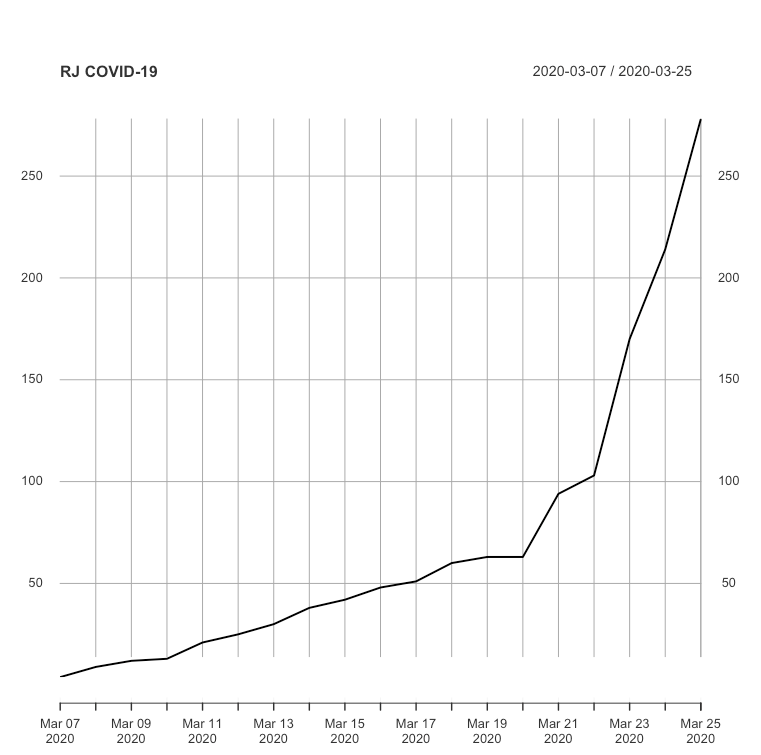
Observando a figura acima podemos perceber que no município do Rio de Janeiro segue comportamento não linear e muito menos estacionário (nem estacionário com tendência). Para ratificar esta observação aplicamos teste Augmented Dickey Fuller (ADF) com hipótese nula de que a série é estacionária ou estacionária com tendência a um nível de significância de 5% (ou 95% de intervalo de confiança). Neste teste, obtivemos o valor Dickey-Fuller de -0,30324 e p-valor de 0,017. Logo, obtivemos resultado estatisticamente significativo de que devemos rejeitar a hipótese nula de estacionaridade e assumir a hipótese alternativa que indica um comportamento explosivo. Este comportamento também foi observado quando realizamos o teste Kwiatkowski–Phillips–Schmidt–Shin (KPSS) tanto para o nível (0,61825 e p-valor 0,021) quanto para a tendência (0, 16473 e p-valor 0,034).
Pelo gráfico acima é possível dividir a série em 3 momentos diferentes:
- Dia 07/03 ao 16/03 onde observamos um “comportamento linear”;
- Dia 17/03 ao 21/03 onde observamos o início de um “comportamento de crescimento exponencial”;
- Dia 22/03 até o momento em que tivemos informação disponível (boletim de 24/03/2020 18:00) onde observamos o início de um “comportamento linear” novamente, mas bem maior que o observado no período de 07/03 ao 17/03.
Assim, para reproduzirmos o comportamento esperado para a próxima semana consideraremos que a base histórica útil à nossa série se inicia no dia 17/03 (quando o total de casos confirmados de pacientes com COVID-19 ultrapassa 50) e perdura até o momento.
Modelos de previsão
Para estimarmos o total de casos de pacientes com COVID-19 confirmados no horizonte de 7 dias a frente (até 31/03) utilizamos modelos univariados consagrados da literatura e regressões apresentados abaixo:
- Modelos de suavização exponencial (ETS);
- Modelos auto regressivos integrados de média móvel (ARIMA);
- Regressão Linear (RL);
Nenhum dos 3 modelos apresentados acima foi concebido para tratar de séries temporais de comportamento explosivo (como é o nosso caso). Entretanto, podemos realizar algumas transformações na série original apresentada para que a série transformada atenda às condições de “contorno” das técnicas apresentadas acima. Neste sentido, as principais formas comumente utilizadas em séries temporais são: diferenciação e transformação logarítmica (elas também podem ser combinadas). Nas figuras abaixo são apresentadas a série original e cada série transformada (logarítmica, diferenciada e logarítmica-diferenciada) de casos confirmados no Município do Rio de Janeiro.
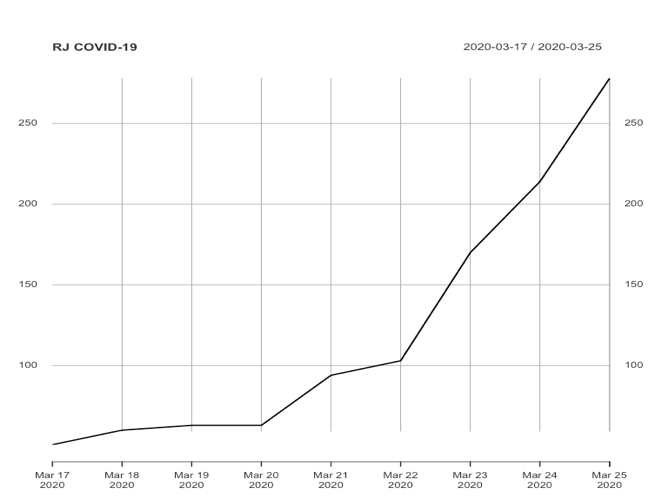
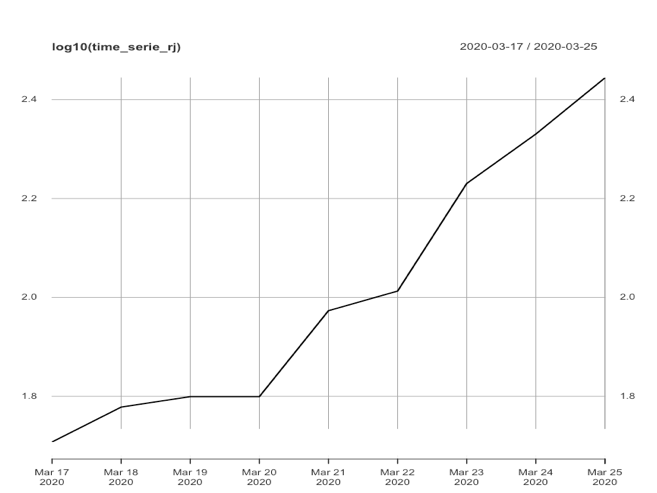
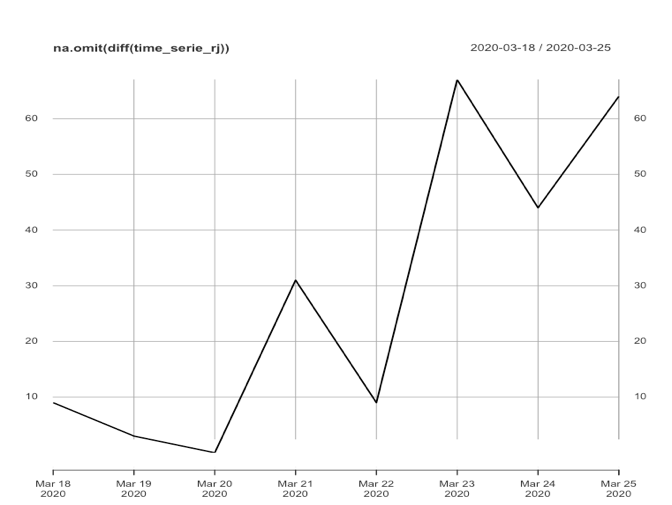
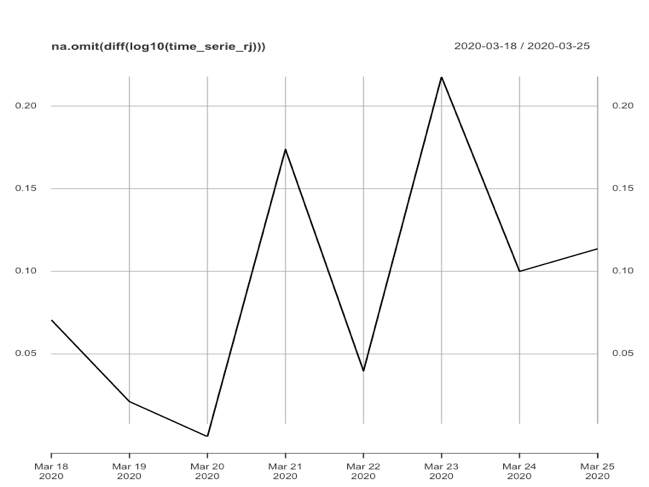
Como o objetivo de trabalhar sobre a série mais estacionária possível (ainda que com tendência) trabalharemos sobre as duas séries que melhor apresentam este comportamento. A partir deste ponto chamaremos as séries escolhidas para prever o total de casos confirmados de série original (SO) e a série “logaritimatizada” (SL) e apresentaremos abaixo características observadas de cada modelos e cada série.
- ETS na série original (ETS SO): não capturou o padrão de crescimento e se manteve constante ao longo do tempo;
- ETS na série logarimitizada (ETS SL): não capturou o padrão de crescimento e se manteve constante ao longo do tempo;
- ARIMA na série original (ARIMA SO): capturou o padrão de crescimento linear;
- ARIMA na série logarimitizada (ARIMA SL): capturou o padrão de crescimento explosivo;
- Regressão linear na série logarimitizada (RL SO): capturou o padrão de crescimento linear;
- Regressão linear na série logaritimizada (RL SL): capturou o padrão de crescimento explosivo;
As previsões otimista, esperada e pessimista de acordo com cada modelo são apresentados nas tabelas abaixo.
| cenário otimista | ets SO | arima SO | rl SO | ets SL | ARIMA SL | rl SL |
| 25/03/2020 | 212 | 323 | 227 | 219 | 306 | 261 |
| 26/03/2020 | 182 | 363 | 252 | 198 | 360 | 322 |
| 27/03/2020 | 156 | 397 | 278 | 184 | 429 | 397 |
| 28/03/2020 | 133 | 428 | 303 | 172 | 514 | 488 |
| 29/03/2020 | 110 | 454 | 327 | 163 | 618 | 600 |
| 30/03/2020 | 88 | 477 | 352 | 154 | 745 | 738 |
| 31/03/2020 | 66 | 497 | 377 | 147 | 900 | 906 |
| cenário ESPERADO | ets SO | arima SO | rl SO | ets SL | ARIMA SL | rl SL |
| 25/03/2020 | 278 | 342 | 257 | 278 | 344 | 303 |
| 26/03/2020 | 278 | 406 | 284 | 278 | 425 | 377 |
| 27/03/2020 | 278 | 470 | 311 | 278 | 525 | 469 |
| 28/03/2020 | 278 | 534 | 338 | 278 | 649 | 583 |
| 29/03/2020 | 278 | 598 | 365 | 278 | 802 | 725 |
| 30/03/2020 | 278 | 662 | 392 | 278 | 992 | 901 |
| 31/03/2020 | 278 | 726 | 420 | 278 | 1226 | 1120 |
| cenário PESSIMISTA | ets SO | arima SO | rl SO | ets SL | ARIMA SL | rl SL |
| 25/03/2020 | 344 | 361 | 287 | 353 | 386 | 352 |
| 26/03/2020 | 374 | 449 | 316 | 390 | 501 | 441 |
| 27/03/2020 | 400 | 543 | 345 | 421 | 643 | 554 |
| 28/03/2020 | 423 | 640 | 374 | 449 | 820 | 696 |
| 29/03/2020 | 446 | 742 | 403 | 475 | 1042 | 875 |
| 30/03/2020 | 468 | 847 | 433 | 500 | 1321 | 1101 |
| 31/03/2020 | 490 | 955 | 462 | 525 | 1670 | 1385 |
Conforme comentado anteriormente, podemos descartar a priori os modelos ETS SO e RL SO porque não foram capazes de capturar o crescimento que devemos prever. Assim, analisaremos apenas os resultados dos modelos ARIMA SO, ETS SL, ARIMA SL e RL SL. Para selecionarmos qual modelo deveríamos usar para estimar a quantidade total de casos esperados para os próximos 7 dias utilizamos os seguintes critérios:
- Teste de normalidade dos resíduos.
- ARIMA SO: p-valor =0, 2987. Não podemos rejeitar a hipótese nula de normalidade.
- ETS SL: p-valor =0, 1987. Não podemos rejeitar a hipótese nula de normalidade.
- ARIMA SL: p-valor = 0,7852. Não podemos rejeitar a hipótese nula de normalidade.
- RL SL: p-valor = 0,259. Não podemos rejeitar a hipótese nula de normalidade.
- Teste de autocorreção dos resíduos (ACF). Apenas a ARIMA SO apresentou auto correlação dos resíduos, mas ela já foi descartada previamente.
- Menor média percentual absoluta do erro (MAPE) dentre os modelos aprovados pelos critérios anteriores.
| Modelos | ME | RMSE | MAE | MPE | MAPE |
| ETS SO | -25,69 | 36,01 | 25,69 | -23,47 | 23,47 |
| ARIMA SO | -6,11 | 25,35 | 18,12 | -7,57 | 16,60 |
| RL SO | 0,00 | 30,07 | 25,75 | -28,25 | 49,88 |
| ETS SL | -25,29 | 35,99 | 25,29 | -22,61 | 22,61 |
| ARIMA SL | -3,78 | 17,66 | 13,18 | -1,24 | 12,43 |
| RL SL | -2,93 | 17,53 | 14,84 | -1,08 | 13,11 |
Desta forma, escolhemos o modelo de ARIMA SL para prever os próximos valores esperados de quantidade de casos confirmados de COVID-19 no Município do Rio de Janeiro. O comportamento explosivo que a nossa previsão apresentou pode ser observado nas figuras e tabela abaixo.
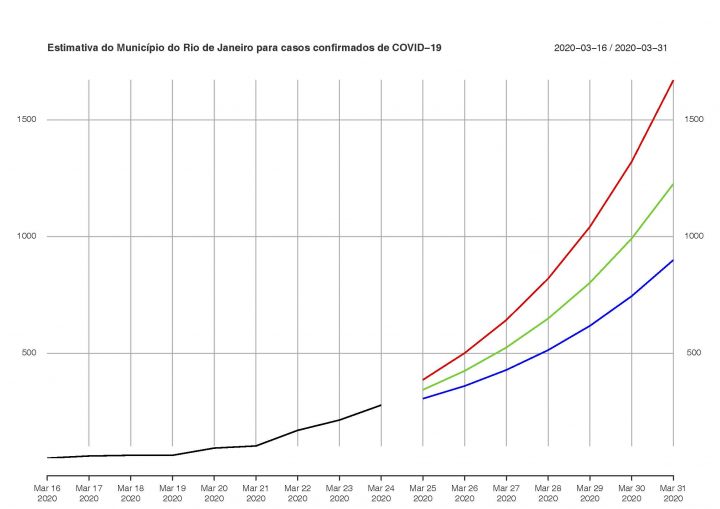
| Dias | Cenário Otimista | Cenário Esperado | Cenário pessimista |
| 25/03/2020 | 306 | 344 | 386 |
| 26/03/2020 | 360 | 425 | 501 |
| 27/03/2020 | 429 | 525 | 643 |
| 28/03/2020 | 514 | 649 | 820 |
| 29/03/2020 | 618 | 802 | 1042 |
| 30/03/2020 | 745 | 992 | 1321 |
| 31/03/2020 | 900 | 1226 | 1670 |
Autor
Daniel Assad
Currículo Lattes: http://lattes.cnpq.br/0258423859812498
Coordenação do LEGOS|UERJ
Profa Thaís Spiegel, DSc. | thais@eng.uerj.br
Currículo Lattes: http://lattes.cnpq.br/8880192361495671