Baixe aqui o texto completo
Nota técnica divulgada em 6 de abril de 2020.
O LEGOS trata o problema de prever a evolução do total de internações de pacientes com síndrome respiratória aguda grave (SRAG) na rede pública (SUS) no município do Rio de Janeiro. Para chegar aos resultados que serão apresentados a seguir utilizamos uma base de dados entregue pela Secretaria Municipal de Saúde (SMS). A série histórica de internações por SRAG em hospitais do SUS é apresentada abaixo.| Data | Casos confirmados | Data | Casos confirmados |
|
16/02/2020[1] |
1 |
11/03/2020 | 17 |
|
17/02/2020 |
2 |
12/03/2020 |
20 |
|
18/02/2020 |
2 |
13/03/2020 |
24 |
|
19/02/2020 |
2 |
14/03/2020 | 30 |
| 20/02/2020 |
3 |
15/03/2020 |
36 |
|
21/02/2020 |
3 |
16/03/2020 |
50 |
| 22/02/2020 |
3 |
17/03/2020 |
84 |
| 23/02/2020 |
3 |
18/03/2020 |
117 |
|
24/02/2020 |
3 |
19/03/2020 | 157 |
| 25/02/2020 |
4 |
20/03/2020 |
189 |
|
26/02/2020 |
4 |
21/03/2020 | 212 |
| 27/02/2020 |
4 |
22/03/2020 |
230 |
| 28/02/2020 |
5 |
23/03/2020 |
267 |
|
29/02/2020 |
5 |
24/03/2020 | 291 |
| 01/03/2020 |
5 |
25/03/2020 |
320 |
|
02/03/2020 |
7 |
26/03/2020 | 333 |
| 03/03/2020 |
9 |
27/03/2020 |
362 |
|
04/03/2020 |
11 |
28/03/2020 | 388 |
| 05/03/2020 |
11 |
29/03/2020 |
408 |
|
06/03/2020 |
11 |
30/03/2020 | 427 |
| 07/03/2020 |
11 |
31/03/2020 |
455 |
|
08/03/2020 |
13 |
01/04/2020 | 462 |
| 09/03/2020 |
14 |
02/04/2020 |
469 |
| 10/03/2020 |
15 |
03/04/2020 |
470 |
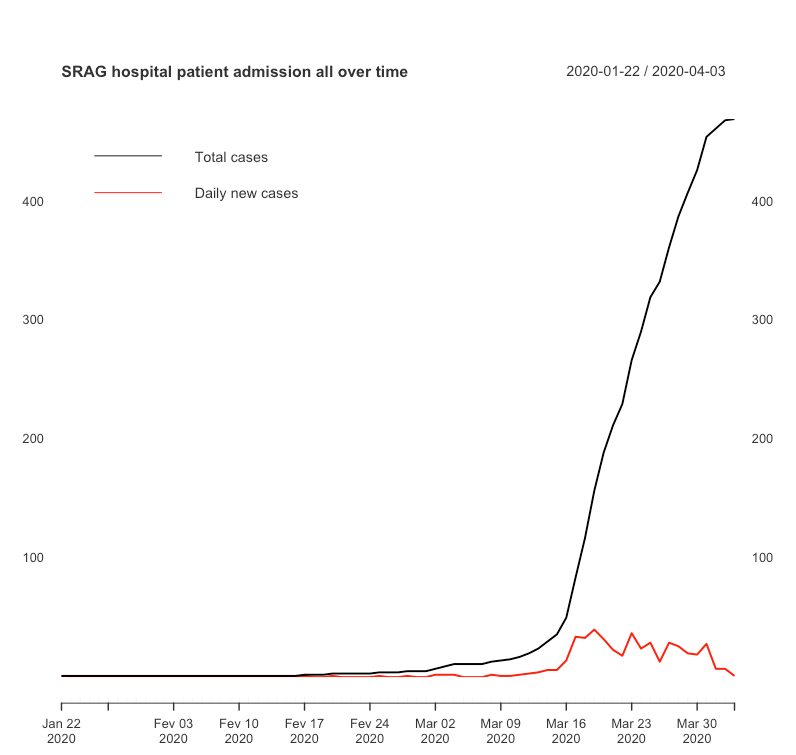 Observando as figuras acima podemos perceber que no município do Rio de Janeiro segue comportamento não linear. Entretanto, se separarmos este gráfico em 4 momentos diferentes podemos observar que:
Observando as figuras acima podemos perceber que no município do Rio de Janeiro segue comportamento não linear. Entretanto, se separarmos este gráfico em 4 momentos diferentes podemos observar que:
- Dia 22/01 ao 01/03 a quantidade total de internações não ultrapassa 5 pacientes
- Dia 02/03 ao 09/03 há um platô por 4 dias (04/03 até 07/03) com média de 1 internação por dia.
- Dia 10/03 até 31/03 a quantidade total de internações cresce abruptamente e depois segue um “comportamento linear”.
- Dia 01/04 até 03/04 a quantidade total de internações cresce menos que o período anterior, mas é causado pela demora de suas notificações por parte das unidades de saúde.
- Modelos de suavização exponencial (ETS);
- Modelos auto regressivos integrados de média móvel (ARIMA);
- Regressão Linear (RL);
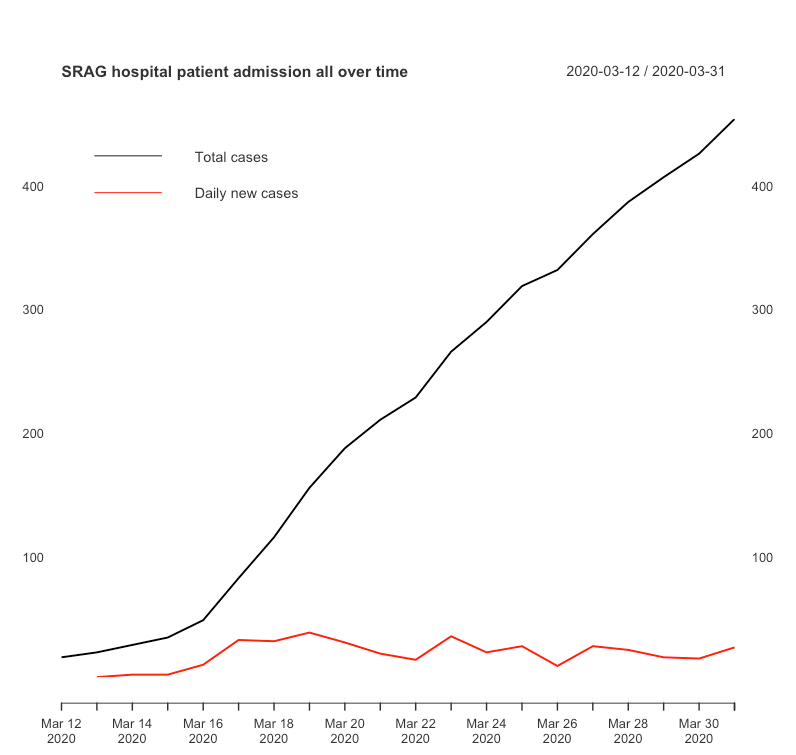
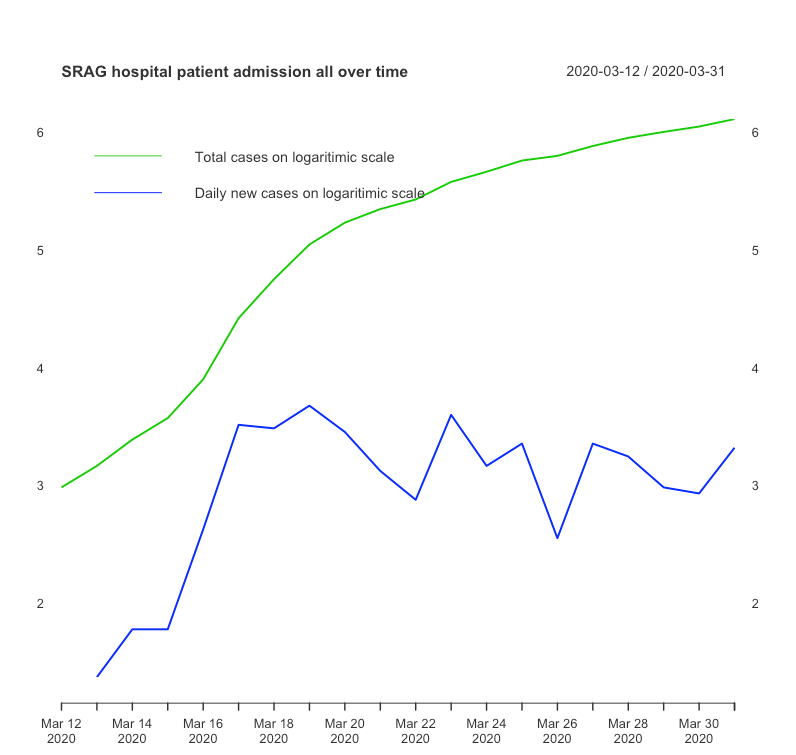 Como o objetivo de trabalhar sobre a série mais estacionária possível (ainda que com tendência) trabalharemos sobre as duas séries que melhor apresentam este comportamento. A partir deste ponto chamaremos as séries escolhidas para prever o total de casos confirmados de série original (SO) e a série em escala logarítmica (SL) e apresentaremos abaixo características observadas de cada modelos e cada série.
Como o objetivo de trabalhar sobre a série mais estacionária possível (ainda que com tendência) trabalharemos sobre as duas séries que melhor apresentam este comportamento. A partir deste ponto chamaremos as séries escolhidas para prever o total de casos confirmados de série original (SO) e a série em escala logarítmica (SL) e apresentaremos abaixo características observadas de cada modelos e cada série.
- ETS na série original (ETS SO): capturou o padrão de crescimento linear;
- ETS na série em escala logarítmica (ETS SL): capturou o padrão de crescimento explosivo;
- ARIMA na série original (ARIMA SO): capturou o padrão de crescimento linear;
- ARIMA na série em escala logarítmica (ARIMA SL): capturou o padrão de crescimento explosivo;
- Regressão linear na série em escala logarítmica (RL SO): capturou o padrão de crescimento linear;
- Regressão linear na série em escala logarítmica (RL SL): capturou o padrão de crescimento explosivo.
- Média igual a 0 pelo teste de Student;
- Segue uma distribuição normal pelo teste de Shapiro-Wilk;
- É independente e identicamente distribuído (não existe auto correlação estatisticamente significativa) pelo teste de Ljung-Box;
- É homocedástico (a variância se mantém constante ao longo do tempo) pelo teste de heteroscedasticidade condicional auto-regressiva (ARCH).
| Teste estatístico | ets SO | arima SO | rl SO | ets SL | ARIMA SL | rl SL |
| Student | 0,68 | 0,77 | 1 | 0,73 | 0,74 | 1 |
| Shapiro-Wilk | 0,85 | 0,67 | 0,34 | 0,36 | 0,38 | 0,06 |
| Ljung-Box | 0,55 | 0,68 | >0,01 | 0,98 | 0,83 | >0,01 |
| ARCH | >0,01 | 0,15 | 0,04 | >0,01 | <0,01 | >0,01 |
| Modelos | ME | RMSE | MAE | MPE | MAPE |
| ETS SO | -1,15 | 12,17 | 9,78 | 19,33 | 24,47 |
| ARIMA SO | -0,61 | 8,80 | 6,98 | 1,78 | 6,85 |
| RL SO | 0,00 | 14,94 | 10,56 | 2,43 | 30,22 |
| ETS SL | 3,32 | 12,32 | 9,79 | 0,31 | 5,80 |
| ARIMA SL | 3,17 | 12,41 | 9,82 | 0,28 | 5,80 |
| RL SL | 11,47 | 93,37 | 63,16 | -5,51 | 30,79 |
| Previsões | ARIMA SO | ARIMA SL | ||||
| Dia | Pessimista | Mediano | Otimista | Pessimista | Mediano | Otimista |
| 01/04/2020 | 492 | 481 | 469 | 535 | 482 | 455 |
| 02/04/2020 | 516 | 505 | 493 | 572 | 514 | 464 |
| 03/04/2020 | 539 | 528 | 516 | 607 | 547 | 491 |
| 04/04/2020 | 562 | 550 | 539 | 649 | 584 | 525 |
| 05/04/2020 | 584 | 573 | 561 | 690 | 620 | 559 |
| 06/04/2020 | 606 | 595 | 583 | 735 | 662 | 596 |
| 07/04/2020 | 629 | 617 | 605 | 785 | 705 | 635 |
| 08/04/2020 | 651 | 639 | 628 | 835 | 752 | 676 |
| 09/04/2020 | 673 | 662 | 650 | 890 | 802 | 718 |
| 10/04/2020 | 695 | 684 | 672 | 948 | 855 | 769 |
| 11/04/2020 | 717 | 706 | 694 | 1015 | 910 | 816 |
| 12/04/2020 | 739 | 728 | 716 | 1079 | 967 | 872 |
| 13/04/2020 | 762 | 750 | 739 | 1150 | 1032 | 928 |
| 14/04/2020 | 784 | 773 | 761 | 1223 | 1101 | 990 |
| 15/04/2020 | 806 | 795 | 783 | 1305 | 1172 | 1055 |
| 16/04/2020 | 828 | 817 | 805 | 1386 | 1250 | 1124 |
| 17/04/2020 | 850 | 839 | 827 | 1479 | 1329 | 1199 |
| 18/04/2020 | 873 | 861 | 850 | 1576 | 1420 | 1276 |
| 19/04/2020 | 895 | 883 | 872 | 1683 | 1511 | 1360 |
| 20/04/2020 | 917 | 906 | 894 | 1787 | 1611 | 1447 |
| 21/04/2020 | 939 | 928 | 916 | 1908 | 1719 | 1547 |
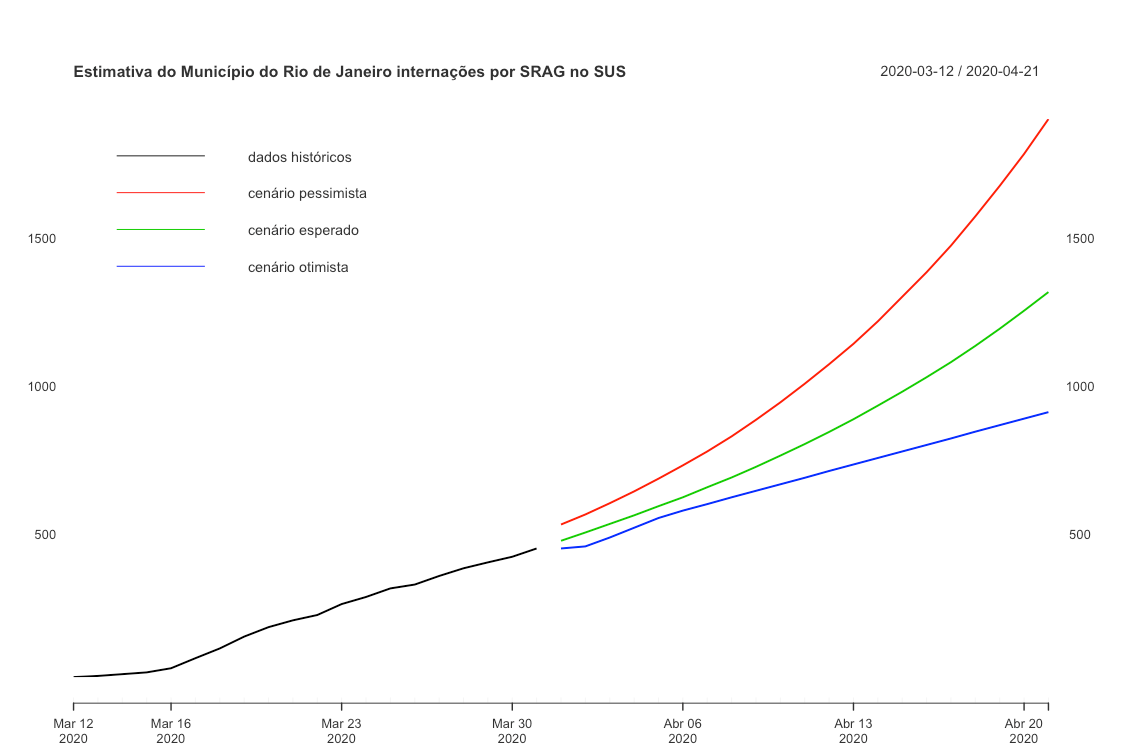 O objetivo dos modelos utilizados foi estimar com a maior precisão possível o total internações por SRAG em leitos SUS em um horizonte de tempo de 21 dias e, com base nos critérios apresentados, concluímos que a combinação dos modelos lineares e exponenciais se mostrou mais adequada.
Não é possível, no entanto, extrapolar este método para um período maior de tempo e nem mesmo concluir, a partir de seus resultados, em que estágio o município está na curva esperada de uma epidemia. Estudos com estes objetivos necessitam de abordagens mais complexas e também são conduzidas dentro do LEGOS.
Previsão de ocupação hospitalar
Com base na previsão anterior para cada cenário o objetivo desta etapa é estimar a quantidade de leitos que deverão ser ocupados caso a previsão acima se confirme.
Como a nossa previsão se deu sobre o total de casos tivemos de fazer a diferença do valor acumulado do dia contra o valor do dia anterior, em outras palavras, contabilizamos apenas as novas internações previstas apresentadas por cenário na tabela abaixo.
O objetivo dos modelos utilizados foi estimar com a maior precisão possível o total internações por SRAG em leitos SUS em um horizonte de tempo de 21 dias e, com base nos critérios apresentados, concluímos que a combinação dos modelos lineares e exponenciais se mostrou mais adequada.
Não é possível, no entanto, extrapolar este método para um período maior de tempo e nem mesmo concluir, a partir de seus resultados, em que estágio o município está na curva esperada de uma epidemia. Estudos com estes objetivos necessitam de abordagens mais complexas e também são conduzidas dentro do LEGOS.
Previsão de ocupação hospitalar
Com base na previsão anterior para cada cenário o objetivo desta etapa é estimar a quantidade de leitos que deverão ser ocupados caso a previsão acima se confirme.
Como a nossa previsão se deu sobre o total de casos tivemos de fazer a diferença do valor acumulado do dia contra o valor do dia anterior, em outras palavras, contabilizamos apenas as novas internações previstas apresentadas por cenário na tabela abaixo.
| Dias | Cenário pessimista | Cenário esperado | Cenário otimista |
| 01/04/2020 | 81 | 26 | 0 |
| 02/04/2020 | 34 | 28 | 7 |
| 03/04/2020 | 38 | 29 | 30 |
| 04/04/2020 | 40 | 29 | 33 |
| 05/04/2020 | 43 | 31 | 33 |
| 06/04/2020 | 45 | 30 | 25 |
| 07/04/2020 | 47 | 34 | 22 |
| 08/04/2020 | 51 | 33 | 23 |
| 09/04/2020 | 56 | 36 | 22 |
| 10/04/2020 | 59 | 38 | 22 |
| 11/04/2020 | 63 | 39 | 22 |
| 12/04/2020 | 66 | 41 | 23 |
| 13/04/2020 | 69 | 43 | 22 |
| 14/04/2020 | 76 | 46 | 22 |
| 15/04/2020 | 83 | 47 | 22 |
| 16/04/2020 | 83 | 49 | 22 |
| 17/04/2020 | 90 | 51 | 22 |
| 18/04/2020 | 99 | 55 | 23 |
| 19/04/2020 | 103 | 58 | 22 |
| 20/04/2020 | 108 | 61 | 22 |
| 21/04/2020 | 118 | 63 | 22 |
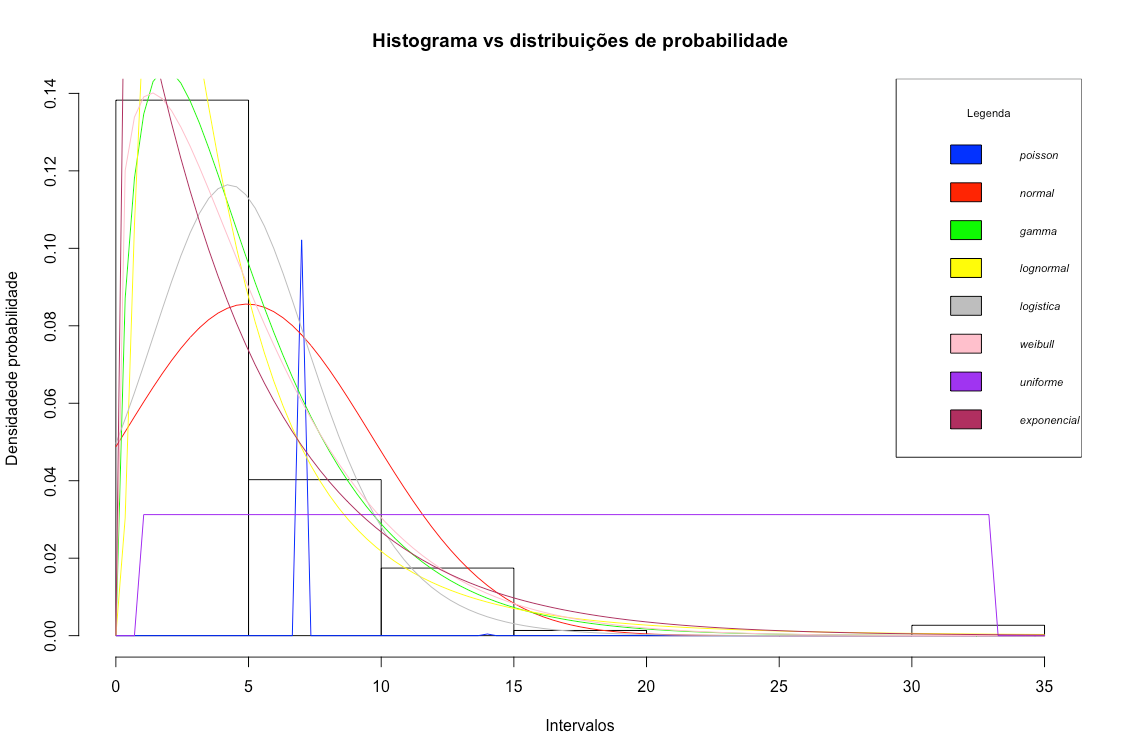 Ao nível de significância de 0,05 apenas são elegíveis as distribuições de probabilidade exponencial (p-valor de 0,745 com rate de 0,20) e weibull (p-valor de 0,053 com shape e scale de 1,23 e 5,33 respectivamente). O tempo médio de internação encontrado foi de 4,95 com desvio padrão de 4,67 dias. Cabe ressaltar que a ambas as curvas encontradas convergem com o que pesquisadores concluíram sobre o tempo de internação em na China e na Itália.
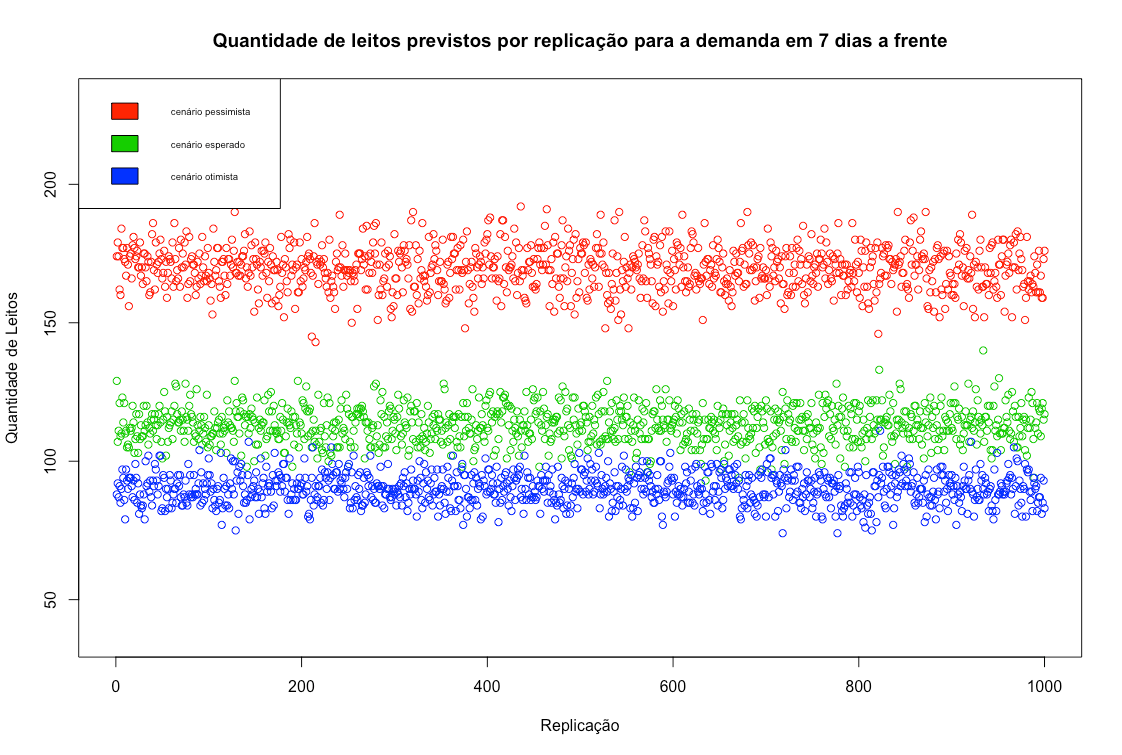
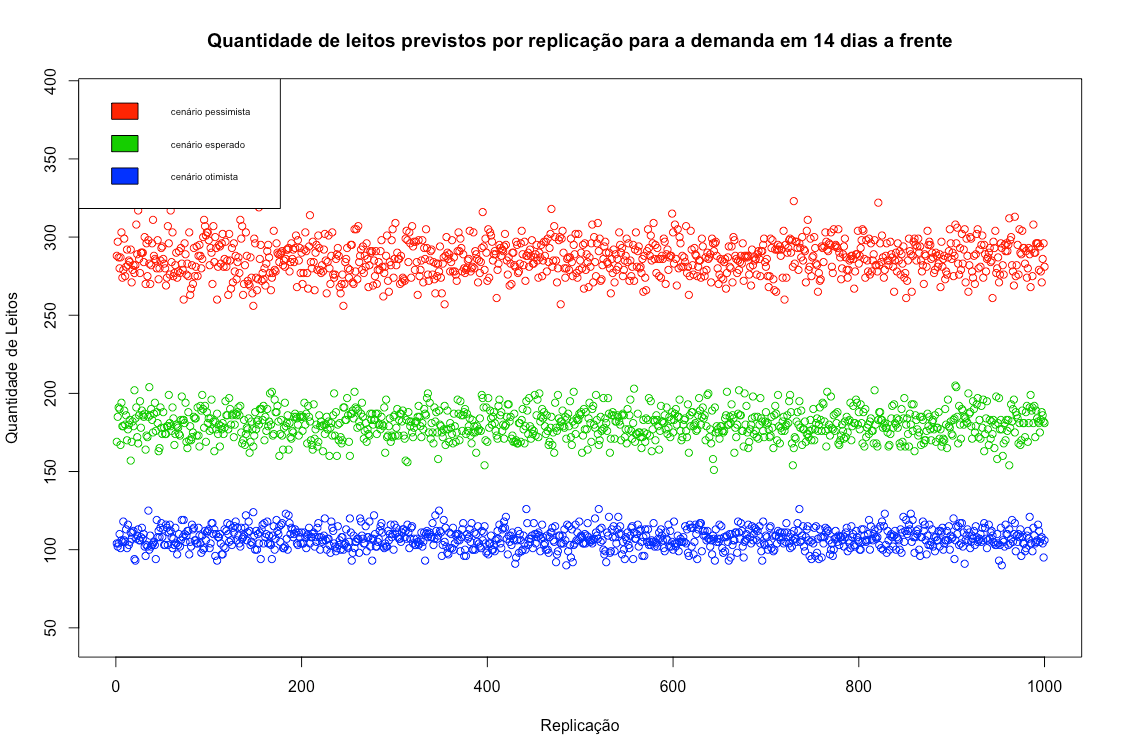
Assim, executando 1000 replicações sobre os valores de cada cenário apresentado na tabela acima chegamos aos resultados apresentados na tabela e figuras abaixo onde nos interessam, em cada horizonte de tempo: o menor valor previsto no cenário otimista, o valor médio previsto no cenário esperado, o maior valor previsto no cenário pessimista.
Ao nível de significância de 0,05 apenas são elegíveis as distribuições de probabilidade exponencial (p-valor de 0,745 com rate de 0,20) e weibull (p-valor de 0,053 com shape e scale de 1,23 e 5,33 respectivamente). O tempo médio de internação encontrado foi de 4,95 com desvio padrão de 4,67 dias. Cabe ressaltar que a ambas as curvas encontradas convergem com o que pesquisadores concluíram sobre o tempo de internação em na China e na Itália.
Assim, executando 1000 replicações sobre os valores de cada cenário apresentado na tabela acima chegamos aos resultados apresentados na tabela e figuras abaixo onde nos interessam, em cada horizonte de tempo: o menor valor previsto no cenário otimista, o valor médio previsto no cenário esperado, o maior valor previsto no cenário pessimista.
| Horizonte de tempo | Cenário pessimista | Cenário esperado | Cenário otimista |
| 7 dias (08/04) | 192 | 114 | 74 |
| 14 dias (15/04) | 323 | 181 | 90 |
| 21 dias (21/04) | 502 | 258 | 94 |
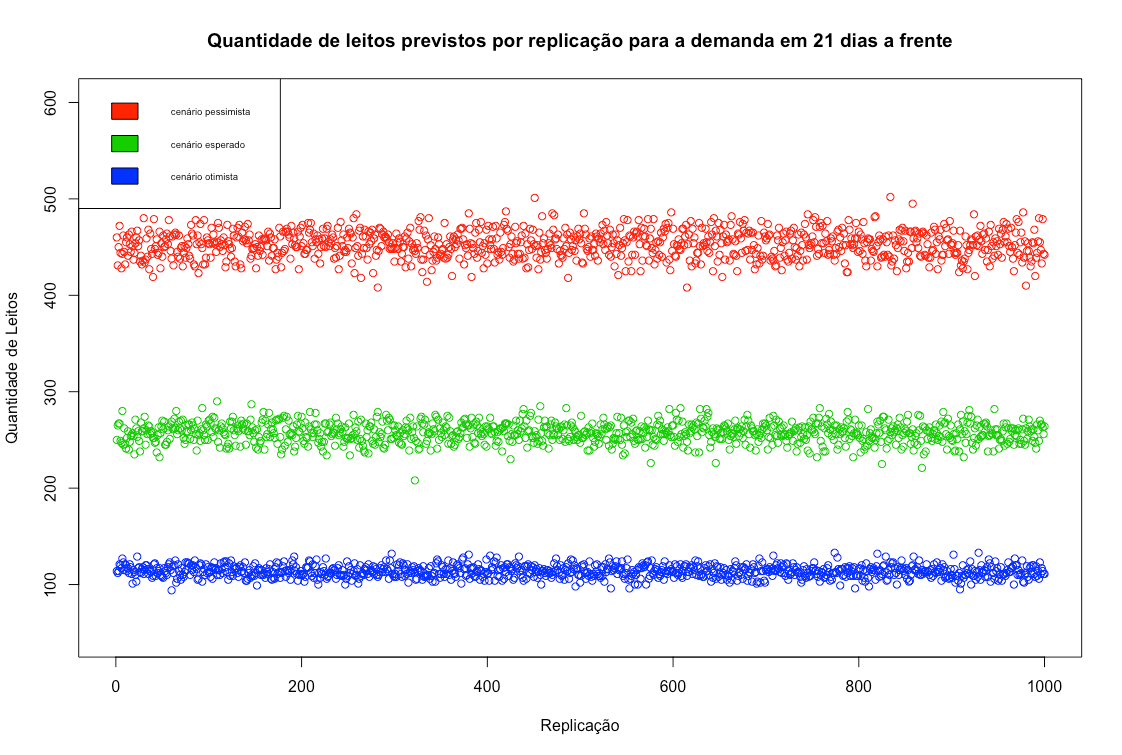 Cabe ressaltar que a grande distância entre os resultados observados em cada cenário ocorre:
Cabe ressaltar que a grande distância entre os resultados observados em cada cenário ocorre:
- Pela mistura de modelos
- Por associar valores de máximo ou mínimo entre ambas as previsões nos cenários otimistas e pessimistas e, no cenário esperado, trabalhar com o valor médio entre as duas previsões.
- Por utilizar percentis muito distantes da mediana nos cenários otimistas e pessimistas
- 381 leitos na etapa 1 em um hospital municipal;
- 85 leitos em hospitais e unidades de emergência espalhadas pelo município;
- 500 leitos em um hospital de campanha em montagem atualmente;
- 300 leitos cirúrgicos sendo convertidos para clínicos.
| Horizonte de tempo | Cenário pessimista | Cenário esperado | Cenário otimista |
| 7 dias (08/04) | Atendido na etapa 1 | Atendido na etapa 1 | Atendido na etapa 1 |
| 14 dias (15/04) | Atendido na etapa 1 | Atendido na etapa 1 | Atendido na etapa 1 |
| 21 dias (21/04) | Atendido na etapa 3 | Atendido na etapa 1 | Atendido na etapa 1 |